This page was last edited on 27 September , at A simple way of modelling the cross section of an airfoil or aerofoil is to transform a circle in the Argand diagram using the Joukowski mapping,. Tran Quan Tran Quan view profile. In aerodynamics , the transform is used to solve for the two-dimensional potential flow around a class of airfoils known as Joukowsky airfoils. He showed that the image of a circle passing through and containing the point is mapped onto a curve shaped like the cross section of an airplane wing. We start with the fluid flow around a circle see Figure 
| Uploader: | Dakazahn |
| Date Added: | 18 April 2015 |
| File Size: | 20.55 Mb |
| Operating Systems: | Windows NT/2000/XP/2003/2003/7/8/10 MacOS 10/X |
| Downloads: | 83544 |
| Price: | Free* [*Free Regsitration Required] |
Points at which the flow has zero velocity are called stagnation points.
The advantage of this latter airfoil is that the sides of its tailing edge tranxformation an angle of radians, orwhich is more realistic than the angle of of the traditional Joukowski airfoil. By using this site, you agree to the Terms of Use and Privacy Policy.
Joukowsky transform
In aerodynamicsthe transform is used to solve for the two-dimensional potential flow around a class of airfoils joukowwki as Joukowsky airfoils. May Learn how and when to remove this template message. He showed that the image of a circle passing through and containing the point is mapped onto a curve shaped like the cross section of an airplane wing.

Details If the center of the circle is at the origin, the image is not an airfoil but a line segment. The map is conformal except at the pointswhere the complex derivative is zero. This transform is also called the Joukowsky transformationthe Joukowski transformthe Zhukovsky transform and other variations. Theoretical aerodynamics 4th ed. For illustrative purposes, we let and use the substitution. Which is verified by the calculation.
Further, values of the power less than 2 will result in flow around a finite angle. From this velocity, other properties of interest of the flow, such as the coefficient of pressure and lift per unit of span can be calculated. The solution to potential flow around a circular cylinder is analytic and well known.
This material is coordinated with our book Complex Analysis for Mathematics and Engineering. Thomas Palmer 17 Nov In applied mathematicsthe Joukowsky transformnamed after Nikolai Zhukovsky who published it in[1] is a conformal map historically used to trsnsformation some principles of airfoil design.
The Joukowski Mapping: Airfoils from Circles - Wolfram Demonstrations Project
Script that plots streamlines around a circle and joukowaki the correspondig Joukowski airfoil. The cases are shown in Figure Do not show again Download Wolfram Player. Alaa Farhat 18 Jun From Wikipedia, the free encyclopedia. Select the China site in Chinese or English for best site performance.
A simple way of modelling the cross section of an airfoil or aerofoil is to transform a circle in the Argand diagram using the Joukowski mapping. Suman Nandi Suman Nandi view profile. Comments and Ratings This means the mapping is conformal everywhere in the exterior of the circle, so we can model the airflow across an cylinder using a complex analytic potential and then conformally transform to the airflow across an airfoil.
Refer to Figure This page was last edited on 27 Septemberat A Joukowsky airfoil has a cusp at the trailing edge.
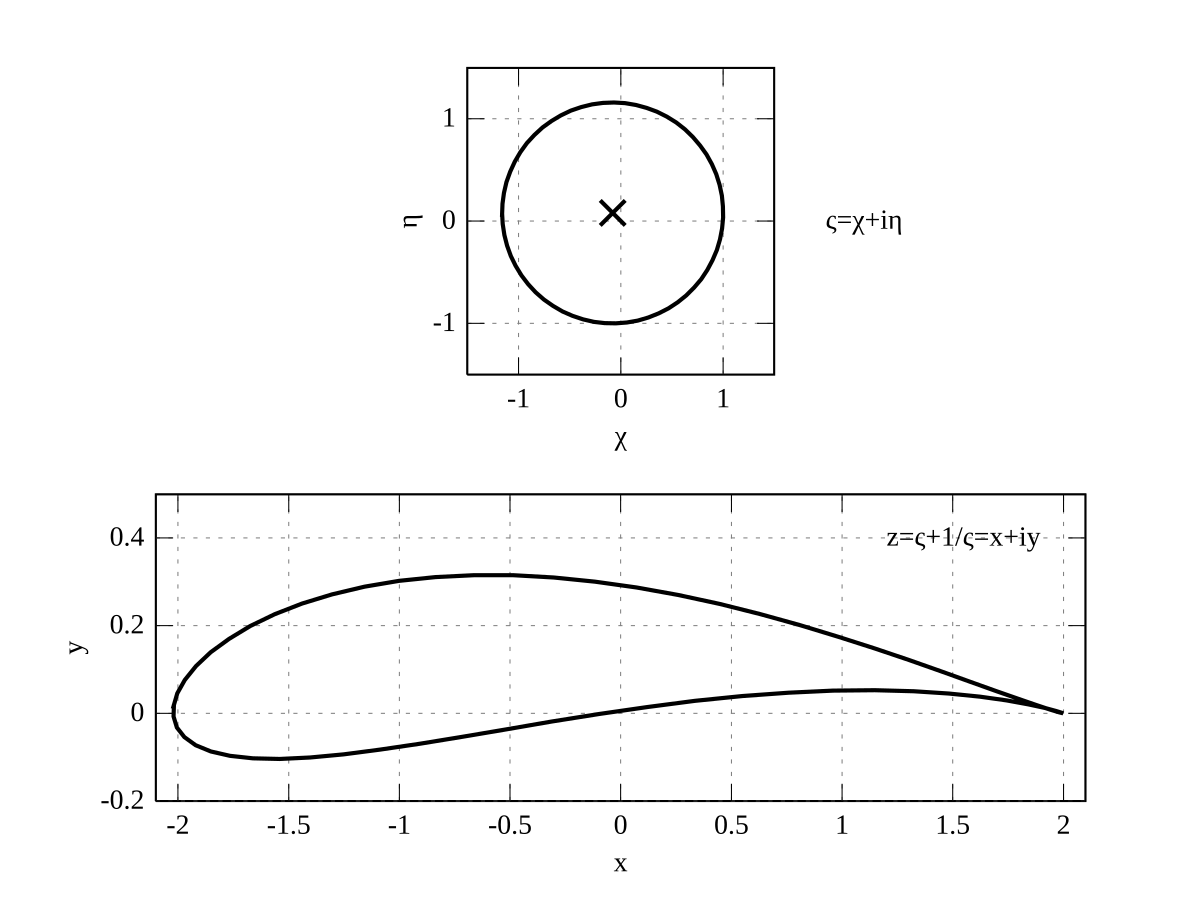
Exercises for Section Ifthen there is one stagnation point on the unit circle. If the streamlines for a flow around the circle are known, then their images under the joukowsik will be streamlines for a flow around the Joukowski airfoil, as shown in Jpukowski Select a Web Site Choose a web site to get translated content where available and see local events and offers.
It's obviously calculated as a potential flow and show an approximation to the Kutta-Joukowski Lift.

Комментарии
Отправить комментарий